Randomness is prevalent in all aspects of gaming and has been part of a love-hate relationship between every gamer in the world. Loots in Battle Royale, draws in Card Games, level or world generation in Minecraft, critical hit chances, Gacha are just some of the random events that are incorporated into video games.
It also goes by a lot of names in the gaming community: luck, RNG, and my favorite one, RNGesus, the lord of random himself. Despite all the awesome and unforgettable moments that randomness has provided to the gaming community, it has been mostly despised, especially in the competitive genre. They argue that RNGs destroy the integrity of games because player decision-making skills are less emphasized, and results can potentially become unfair or skewed. In truth, however, most developers out there have carefully balanced the random factors in their games, and our unlucky streaks might just be a result of our cognitive biases.

No one ever complains when they expect a bad result but is saved by RNG. However, when RNG flips us over just one time, we often amplify our unfortunate outcome and claim that the game is unfair. Our brain also handles probability incredibly poorly. A 90% crit chance can feel like 99%, even though the two percentages are vastly different. 90% means that you will NOT deal critical damage 1 time out of 10 hits. 99% means that you will NOT crit 1 time out of 100 hits. These biases generate a lot of hate towards randomness in general and force developers to use RNG very carefully. However, in this article, we will be diving into the concept of randomness in great detail that will hopefully help to gain some insights and clear out all the misinterpretations that come with this topic.
Why put randomness in games?
Before we try to closely find out what randomness means, I think that it would be very beneficial if we establish the reasons why the concept is applied to gaming in the first place. Firstly, randomness has the capability to provide variety, diversity, quantity, and essentially makes the game less boring. Minecraft worlds, for instance, are always unique and infinite; no two world’s seeds are the same. Draws in card games also ensure that matches play out differently.
On the flipside, Chess has no randomness, and many games have been repeated with the same order of moves. Chess also suffers from paralysis of analysis, where players can almost predict the next set of moves due to the absence of randomness. Of course, this fact does not imply that chess is a poorly designed game, but I think that many do agree that it can sometimes be boring. Randomness can solve the paralysis of analysis because it creates a fog that limits the information given to the players. They can not fully predict the future, but only make plays with the highest probability of succeeding. As a result, they can’t entirely memorize the game and instead focus on the fundamentals.
We can also see the distinction between random and non-random games in the two popular types of Minecraft speed runs: set seed vs. random seed. Set seed speed runs to ensure that players spawn in the same exact world and position. There is almost no randomness involved, and speedrunners can memorize all the tasks they need to do to complete the run. Random seed speed runs, on the other hand, are filled with surprises. Player’s have no clue about the world they spawn in, where the ender dragon is located, and all the shortcuts they can take to massively shorten their time. Therefore, players are forced to master the fundamentals of Minecraft and find creative optimal strategies, whether it is going to a Bastion, trading with villagers, using TNTs to explode jungle trees, and whatnot.
Other than providing variety, randomness can also introduce balance into games. For example, Mario Kart loot boxes favor players behind and give them the chance to catch up. Of course, this concept must be carefully implemented since randomness also has the potential to create imbalances, allowing less-skilled players to beat the more proficient ones.
RNG can also provide the element of thrill. Rarity is often part of an exciting playing experience, especially in the addicting Gacha games. Furthermore, random factors have the potential to enforce a unique playstyle. In CS:GO, weapon spray patterns are not random, which is why spraying is prevalent. Its counterpart, VALORANT, has spray patterns with minor uncertain variances, so players more often tap and burst than simply committing to a spray. However, VALORANT is much more forgiving in terms of the random bullet spread when running and gunning, which is why players can run and gun in close quarters. CS:GO bullet spreads are impossible to predict when moving and no one run and guns in this game.
Lastly, randomness can also urge players to take certain objectives and calculate risk. Dota 2 players, for instance, constantly fight to take the high ground for two reasons: vision and uphill miss chance. Ranged heroes are extremely unfavored when fighting in the low ground because they have a 25% chance of missing when hitting enemies on the high ground. However, being in the high ground can sometimes sacrifice positioning and enable enemies to close the gap. Therefore, players have to decide whether they should risk being jumped on or miss a quarter of their auto-attacks.
What is Random?
Random is often misinterpreted and misunderstood by a lot of people, which is why I think it is important to discuss it here. You might that randomness is synonymous with unpredictability; well this notion is completely false. All random events are, for the most part, predictable with the help of probability. When you toss a coin, you will have a 50% probability of the coin landing on heads. Therefore, if you toss a coin 200 times, it is very likely that 100 of those flips will land on heads. The same exact concept applies to Random Number Generators (or RNG) in computers. If you ask a computer to generate a random number from 1 to 100, you have a 1/100 chance of the computer outputting the number 42. However, RNGs beg a much more important question: how do computers simulate randomness?
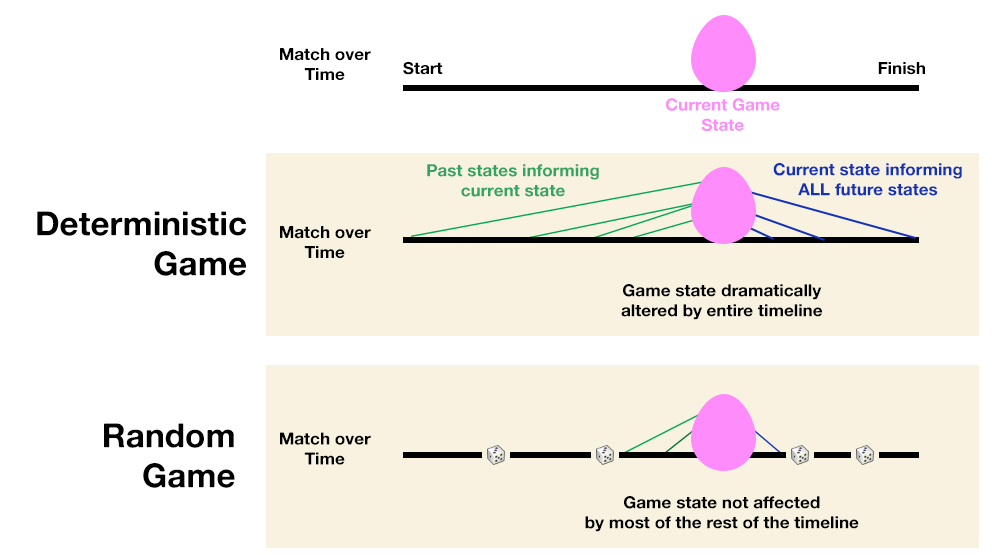
We often classify a coin toss as being random because we cannot fully know the outcome. But in a hypothetical situation, we could, in fact, find the result of the coin toss after it is flipped to the air. We will just have to calculate all the forces present using some maths and physics. It is undoubtedly difficult to do, but it is not impossible. Researchers have even created coin-flipping robots that could get the same coin-flip results almost every single time, concluding that “coin flips are physics, not random”. As a result, the coin flip system is dubbed as deterministic. In other words, we can predict the future state of the system if given all the initial conditions. But deterministic systems can still seem random. If the system is too complex and would take far too long to calculate and predict, the system would seem random to the naked eye. A coin toss can technically be predicted but is simply impossible to calculate in a real-world scenario.

Computers are undoubtedly very predictable and deterministic. However, we can make computers generate seemingly random numbers using the idea of complex systems. RNGs that we often refer to in games usually use pseudo-random number generators that use mathematical functions or algorithms to mimic randomness. If we know the seed (the initial condition), we could predict all the “random” numbers that the computer will spit out. There are other ways in generating random numbers in computers that avoid the seed loophole, such as using atmospheric noises. But for most games and software, pseudo-random numbers are the most convenient method of simulating randomness in predictable computers.
The two types of Randoms in Statistics
There are also two types of random or probability in the field of statistics: dependent and independent. It is important to distinguish the two of them because they can highly impact decision-making in games and even game design or balance. Independent events mean that one event does not affect the probability of another event. For instance, you will get a 50% chance of getting tails in the first coin toss and the same 50% chance in the second coin toss. Dependent events are the opposite; separate events influence each other’s probabilities. If you draw from a normal deck of cards, you have a 4/52 chance of drawing in King. If you don’t draw a king on the first draw, you will have a 4/51 chance of drawing a King on the second draw.
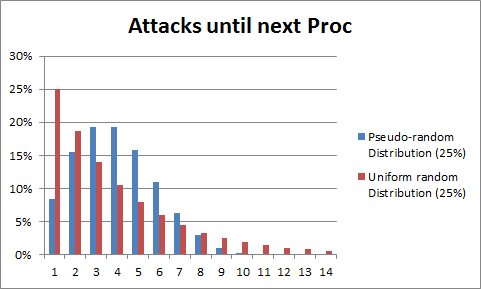
Dota 2 has experimented with these two kinds of randomness in the past. Back then, all random values in Dota had a uniform random distribution (or independent). If you have a 25% to deal critical damage, that 25% chance will stay constant throughout all your auto attacks. In a later patch, however, they implemented the pseudo-random distribution (don’t confuse this with the pseudo-random number generator) or PRD to simulate dependency. Let’s say you still have that 25% chance to crit. On your first hit, you will actually only have an 8.5% chance to deal critical damage. If you did not crit, the percentage increases to 17% on the next hit, and 25.5% on the next, and so on. If you hit the crit, the percentage resets to 8.5% again. In the long run, using PRD still average the crit chance to 25% but with much greater consistency. According to the devs, the PRD mechanic helps induce less luck-based gameplay.
Since the highly competitive Dota 2 is riddled with tons of RNG, the community is very lucky to have Valve taking a look at the importance of statistics in the game. Without the update to the random system in Dota 2, we might still see “highly skilled” Phantom Assassins two-shotting supports and the infamous 17% Spirit Breaker bashes.
Where to place randomness in games?
Game developers often classify or place random events based on player decisions. After all, games are just a series of player decisions in a period of time. Randomness in gaming is either located before or after a player makes a decision and inputs a move. A random event that occurs BEFORE the player makes a decision is called input randomness. Examples of these are draws in card games or Minecraft world generation. A random event that occurs AFTER the player makes a decision is called output randomness. Lootboxes, critical hit chance, and run-and-gun bullet spreads fall into this exact category.
Output randomness is one that is often referred to as RNG. Gamers mostly hate this type of random since it reduces control over an expected outcome, and thus developers must carefully balance it. We have previously seen what Valve did with their critical chance output randomness. Justin Ma, the co-founder of Subset Games, also mentioned that he only incorporated the less volatile types output randomness when developing Spelunky. The developer team intentionally did this to make the game potentially less frustrating for players.
Input randomness also plays a part in the strategic aspect of games, but it certainly does much less harm since the players still can react to the random event. However, this does not suggest that input randomness can just be left ignored or unadjusted in game design. In Hearthstone, if you start your game holding high mana cards, you will most likely not survive for long, especially against an aggressive opponent. To deal with this input randomness, the devs implemented a mulligan system where you can choose to replace any card in your starting hand with a random card in the deck. If you know you will need to fight for the early game, you can conveniently mulligan out high mana cards in your hand and hopefully get replaced with a much lower mana card.

Conclusion
By now, you should have a basic understanding of the concept of randomness, probability, and how they are applied in the realm of video games. You have also gained some insights into why developers love to incorporate random elements in their games. With all this newfound knowledge, you can now hopefully improve your in-game decision-making skills by taking into account the random factors that might come into play. More importantly, however, you can now understand and be less triggered when RNGesus decides to screw you over.
Featured Image: Unsplash













